Brief Introduction

We propose a novel quaternion product unit to represent data on 3D rotation groups. 3D rotation can describe the movement between two 3D vectors. For example, a 3D skeleton can be converted into joint rotations. 3D rotation data are not closed under additions and multiplications used in standard neural networks. Our insight is to use the law of 3D rotation group to ensure this closure. On the other hand, quaternion algebra gives an elegant way to describe 3D rotations.

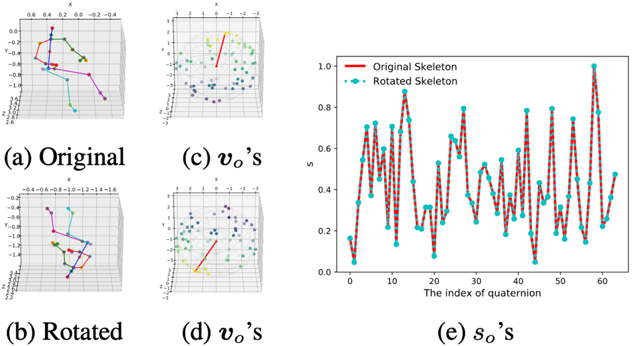
The proposed Quaternion Product Unit, or QPU, represents 3D rotation data as quaternions and merges them via a weighed chain of Hamilton products. We prove that the output of QPU can be disentangled into "rotation-invariant" features and "rotation-equivariant" features.

We design QPU-based neural networks and make our models compatible with existing deep learning models. We conduct experiments on 3D skeleton-based action recognition task. Experiments on both synthetic data and real-world data show that the proposed QPU is beneficial for the learning tasks requiring rotation robustness.